Exploiting Weak Randomness in the Croupier-Spun Wheel of Fortune

Randomness exists in gambling as a necessity, and the games are constructed so as to provide randomness (excepting, of course, fraudulent games). Gamblers have always sought for and chased objectively or subjectively “breaches” in the randomness of the games on the basis of which to develop strategies so as to gain an advantage over the house. The question is whether such games exist and how their fairness is exploitable, and in particular, if the Wheel of Fortune randomness is weakened show game.
Random Generation of Outcomes from Dice to the Wheel of Fortune
The technical processes by which games of chance function in regard to the generation of their outcomes start with a process chosen so as to cancel any possibility for information about causes and initial conditions that determine the outcome. This primary process may be spinning (reels, the roulette wheel, and the Wheel of Fortune), shuffling (card decks or balls), rolling (dice), tossing (coins), or mixing (tickets or other objects) and fulfills its role through physical features such as high speed, intensity, non-equilibrium, and/or non-visibility.
The complexity of the physical factors involved in these technical processes, among which some are external and circumstantial (such as the air current and heat in the room, the player’s breath, the vibrations of the floor, etc.), makes objective analysis yielding accurate predictions almost impossible.
The physical process of generating the outcomes of the games in the condition of randomness was replaced in modern games by electronic devices and software simulating the original process. All online casinos offer classical games in electronic versions, where the generation of outcomes (such as spinning, shuffling, etc.) is done electronically using special software called a “random number generator” (RNG).
The goal of such software is to generate numbers randomly to be assigned to the outcomes of the game—that is, by no rule of determination for the next coming number and with no dependence on the previous numbers.
The Old-Fashioned Wheel of Fortune in the Modern Version
That being said, some games of chance in casinos are still operated by croupiers. Roulette is the most popular example; however, by its physical construction, no alteration of randomness can be assumed in any statistical analysis of the game. Indeed, the spinning of the wheel, combined with the throw of the ball in whatever parameters of magnitude, still makes a deterministic approach based on physical factors to predict where the ball will land impossible. This impossibility comes from the fact that the roulette wheel’s rotations at a spin are in the order of tens and that the number of revolutions of the ball is still in the order of tens, giving a number of “combined” rotations in the order of hundreds. The relative speed of the ball to the wheel is also very high, given that the rotations combine in opposite directions.
A less popular game of chance operated by a croupier—having its origin in old country fairs, being popularized by famous television shows, and resembling roulette—is the Wheel of Fortune. Unlike roulette, the Wheel of Fortune spins in a vertical position and has a significantly bigger diameter and weight; this is also the reason why the croupier spins the wheel a very limited number of times (usually between 2 and 5 rotations).
The current analysis is made for a modern version of the Wheel of Fortune present in some casinos, described in what follows.
The wheel has 54 segments labeled with 8 possible outcomes on a spin, namely, numbers 1, 2, 5, 10, 20, and 40, as well as multipliers M1 and M2. Players may bet on any of the 6 numbers within the table limits. The payout rate is different for each of the 6 numbers as follows:
Table 1. Payout Schedule
The multiplier segments make the game more interesting. If the wheel stops on the M1 or M2 segments, new bets are not accepted, and the wheel is spun again. Any wins on the next spin are multiplied by a rate specific to M1 or M2 (different versions of the game have different multiplying rates).
The croupier starts spinning the wheel before the betting time is over and continues for several seconds after that moment.
Is the Croupier a Good “RNG”?
Full electronic and croupier-free roulette games spin their wheels electronically, the former having their outcome determined by RNGs. The physical Wheel of Fortune remained operated by a croupier as it is in the game’s tradition; although there are electronic versions of the game, the game in its traditional form is more enjoyable and interesting.
Given the low number of rotations and the low rotation speed, one can fairly hypothesize that once the initial position of the wheel is known, certain segments of the wheel have higher chances of winning, and a player could benefit from this information. How random the spin is depended, of course, on the number of rotations, which, in turn, depends on the croupier’s arm strength and other factors.
The question is whether such a spin is random enough to prevent any strategy based on physical observation and objective analysis and, if not, how such a strategy should be elaborated to work.
The table below shows the probability and house edge for every possible bet in assumed conditions of randomness.
Table 2. Probability and House Edge
Observe that the house edge is neither equal over the bets, as in roulette, nor proportionally increasing with the payout rate. The house edge of roulette is about 7.3 lower than the average house edge of the bets in the Wheel of Fortune.
Could the house edge be reduced by strategies relying on proven weaker randomness—that is, knowing that some segments are more probable than others?
Even though the wheel rotates a few times and relatively slowly, these conditions are not enough to make a deterministic analysis by which to yield accurate predictions. The multitude of the physical factors involved is still huge for being quantified into a predictive theoretical model.
Thus, the only alternative available for an objective analysis remains to be statistical inference. Computer scientist and security analyst Jesús Miguel Calderón Marín carried out statistical work for this game to answer the questions above.
Statistical Analysis for the Wheel of Fortune
The statistical test in the discussion was based on a recording of 7,278 spins and involved the following variables:
- Winning number (the outcome of every spin)
- Absolute position (the unique number identifying every segment of the wheel—e.g., the yellow segment has absolute position 0, proceeding counterclockwise up to 53)
- Winning absolute position (the absolute position of the winning number)
- Direction (the direction in which the wheel is spun—“clockwise” or “anticlockwise”)
- Positions run (the number of wheel rotations multiplied by 54)
- Hand time (the moment when the spin starts relative to the beginning of the video recording, in seconds; it is associated with the initial position of the wheel as the segment aligned with the outcome pointer)
- Relative positions (unique numbers identifying the segments standing in the initial position—1 is assigned to the top position; the next segment as position 2 is on the left of position 1 if the wheel rotates clockwise and on the right otherwise)
- Winning relative position (the relative position of the winning segment)
Among these variables, only three are related to the physical conditions of the spin: direction, positions run and hand time. The value of the “positions run” variable reflects the strength of the spin and the number of rotations.
The values of the variables “winning absolute position,” “winning number,” and “winning relative position” were analyzed through a chi-square test of independence to decide whether they were random. The first two variables have passed the test successfully, indicating that the difference between the analyzed number distribution and the expected distribution is attributed to good luck and not to the lack of randomness. This means that we cannot state that the winning numbers are not randomly drawn, that there is a difference in the size of the segments, or that the wheel is biased.
The surprise was instead for the values of the “winning relative position” variable. The data revealed the critical value exceeding the chi-squared statistic (from 79.84 to 90.75), suggesting that this variable is far from random, especially for spins in the clockwise direction. For instance, it was estimated that relative position 29 has a probability of being the winning position of 2.15% (instead of the expected 1.85% in conditions of randomness). This lack of randomness in the Wheel of Fortune could then be exploited by players.
With this new probability, the house edge for this bet goes down to 11.85% compared with the initial 24.07%.
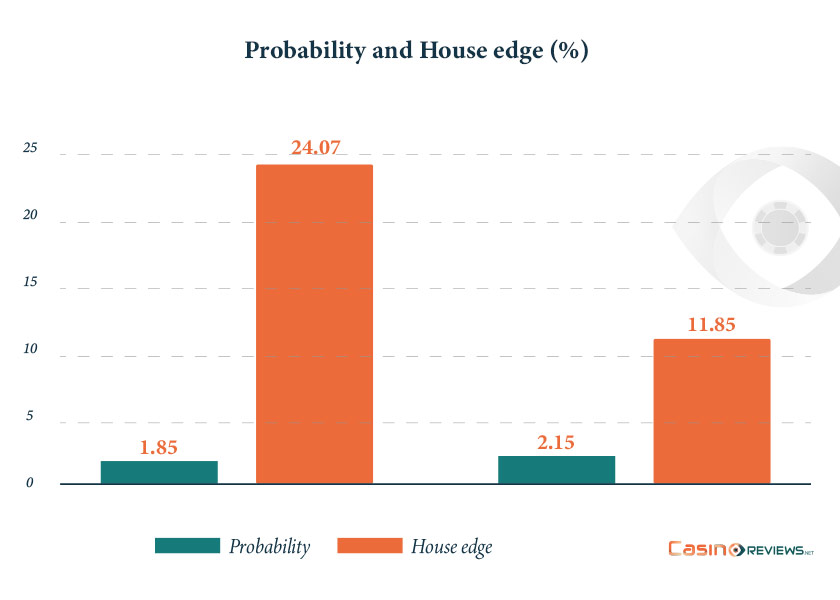
Chart: Probability of Winning and House Edge for the Bet on Segment in Relative Position 29 in Random vs. Favorizing Conditions
Strategies Exploiting the Lack of Randomness
The author of the statistical analysis has also designed basic strategies that could exploit the detected lack of randomness.
The simplest strategy is to track relative position 29 as offering the highest winning probability when the direction of the spin is clockwise and to associate it with the highest payout rate.
This means to bet on number 40 if that segment is in relative position 29 in the clockwise spin and skip the bet otherwise. With this strategy, it was estimated that the player could get a return ranging from 0.56% to 41.80%—that is, they could win a minimum of $5.6 to a maximum of $418 at every $1,000 bet with about 90% confidence.
Another strategy is to bet on number 10 (as the bet with the lowest house edge among those with higher payout rates) when number 40 is in relative position 39 and keep the bet on number 40 when it is in relative position 29. It is worth noting that such strategies might require a long time to produce real gains since so many games are discarded when tracking only one or two segments to match one relative position.
In addition, the bets need to be made automatically since it is almost impossible to count the positions, make the betting decision, and place the bet in the very limited time available.
More elaborated strategies can be designed to involve not only the number 40 but also several or all the numbers on the wheel. Such strategies would provide, for every relative position of number 40 as the reference point, the best number to bet on or the indication not to bet, and this would be different for clockwise and anticlockwise spins.
The author of the analysis also assessed the effectiveness of such strategies using statistical methods based on Monte Carlo simulations and found that they all provide greater returns for the player than random strategies.
Statistical inference is an objective method of investigating hypotheses and making predictions, but it does not provide absolute certitude, such as deterministic deductive methods. However interesting or unexpected the results of statistical analysis, there will always remain open questions such as “Is this really so?” or “Was the number of recordings large enough?” Contrary to popular belief, in gambling analysis, “size does matter”; however, no science can tell us precisely how large this number should be to attain sureness.
If the discussed statistical analysis of the croupier-spun Wheel of Fortune reflects reality, the only test it still has to pass is that of the players—the real effectiveness of the strategies based on the assumed breach of randomness. However, such tests are hardly traceable and decidable. As in other games of chance, objective strategies may reduce house edges, but the outcomes still obey the probability laws, including the Law of Large Numbers. So we must not be so excited when we reduce a house edge twice by strategy for at least two reasons:
- The reduced house edge still may be higher than in the other games available.
- The number of plays needed for materializing the difference is still reflected in the probability of winning and, as such, may be huge. There is always a balance among these factors, and this is not in the players’ favor; hence, luck cannot be taken out of gambling.
References:
Marín J. M. C., 2022. Wheel of Fortune Outcome Prediction — Taking the Luck out of Gambling. NCC Group Research, August 2022.








Review this Blog
Leave a Comment
User Comments
comments for Exploiting Weak Randomness in the Croupier-Spun Wheel of Fortune