Gambling Math in Action – The Martingale Betting System in Roulette

The struggle to beat roulette over the history of gambling has led to the conception of all sorts of betting strategies or systems, and in this exercise, simple players and game theorists were involved as well. For the static bets (that is, bets with constant parameters whose expected profit is relative to one game), almost everybody came to know that expected value is negative and that over the long run, roulette’s house edge is approached.
Then mathematicians investigated how things change if the bets are repeated with a modification in their parameters in every new game following a loss while aiming at an overall profit over an indefinite series of plays. This is how they arrived at the so-called progressive betting systems, which can be played not only in roulette but also in other games of chance such as blackjack that offer the minimal conditions for them to be effective. The most popular is the martingale system, and today we will focus on its implementation in roulette betting.
What Is a Martingale?
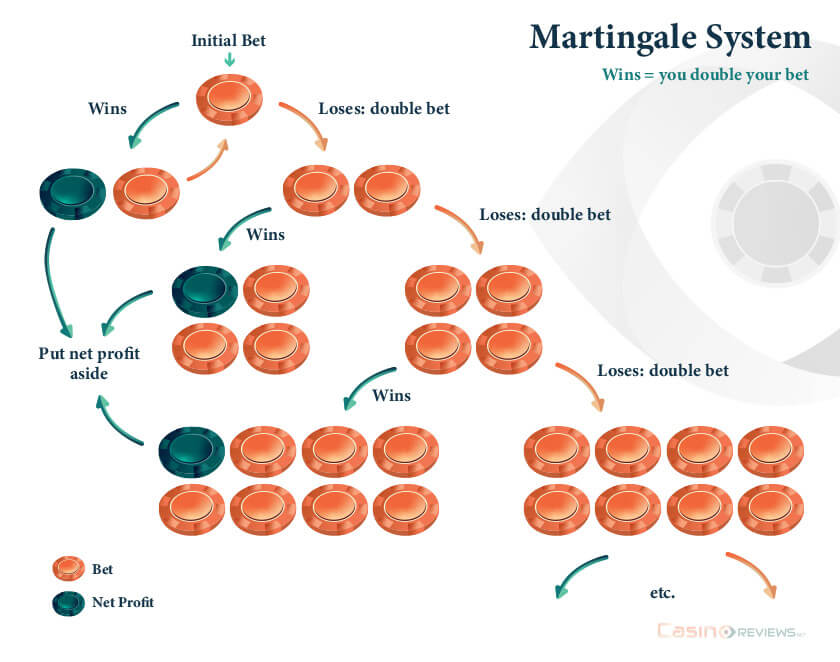
In general, a martingale system assumes that the same bet is played repeatedly while raising its stake with a multiplier at every new game if the previous bet is lost. For example, you bet $1 on red. If you win, stop and continue if you want with whatever bet. If you lose, place the same bet on red at the next spin with a stake of $2. If you win, stop or continue as you want. If you lose, place your bet on red with a stake of $4, and so on. The idea is to double your stake after each loss.
In our example, the bet was on color, and the multiplier of the stake was 2; however, theoretically, you may choose any kind of bet and any multiplier to have a martingale. Still, what does mathematics have to say about this?
The “Optimistic” Math of the Martingale
Surprisingly, pure mathematics—which, through the probability laws, tells us that no winning strategy over the long run is possible for any game of chance—credits the martingale to be a sure winning strategy over the plays from the first bet to the first winning bet no matter the stake or the multiplier used. How is that possible? It is due to a simple algebraic certitude. Let’s stay with the bet on color and let S be the stake of your initial bet. Assume that n consecutive bets are lost and that the n + 1-th bet is won. The total amount lost before the n + 1-th bet is S + 2S + 4S + ... + 2n-1S = S (2n - 1) < 2n S, and the last term in the inequality is the stake of the n + 1-th bet, assumed won and proven to be less than the total amount lost. Of course, the same result holds for similar types of even/odd or low/high bets.
This mathematical certainty also holds for other types of bets and other multipliers. If you choose 3 as the multiplier instead of 2, the total amount lost over n losing bets is less than 3n S, which is the profit of the n + 1-th bet. Also, if you choose a column bet instead of a color one, the mathematical relation becomes S + 2S + 4S + ... + 2n-1S = S (2n - 1) < 2n S < 2n+1S = 2 . 2nS; observe that the last term is the profit of the column bet won, exceeding the cumulated loss.
With this mathematical proof, the system seems infallible: whatever succession of losses will end at some point, and the next win will make you a profit. Furthermore, the probability of having a long succession of reds or blacks is very low (if such information counts in any way). Still, why doesn’t everybody play this system, and why has roulette not been declared beaten by now?
Constraints and Weaknesses
In the mathematical relation above, we focused on the last term, reflecting the profit of the last bet, but the sum in the left-hand member reflects the cumulated loss. With only $2 as the initial stake and five consecutive losses, it reaches $60. For ten consecutive losses, it reaches $2,046. The mathematical relation also gives us the overall profit: 2n S - (2n - 1) S = S. Hence, the net profit of such a progressive bet is S, whatever the number of consecutive failures, and this amount is actually the goal of the bettor.
If you start with $2, you will win $2 in the end (exactly like you would have won with a static color bet). If you don’t win from the start, the amount lost begins to accumulate, and the longer the series of losses, the lower the profit rate when a win occurs. In our example above, with a loss as the investment of $60 for five failures in a row, the profit rate would be only 3.33%, under the assumption that you have that $60 to sustain the loss plus another $64 to place the next winning bet. For a goal of $50 in profit, you will have to start the martingale with this stake; if four consecutive failures occur, you have to sustain a loss of $750 and a new bet of $800.
Therefore, real-life circumstances seem to threaten the effective application of that mathematical certainty related to the martingale. First, it is about the size of your bankroll, which should be large enough to sustain a loss as a result of a hypothetical long succession of failures. Limiting the cumulated loss has imposed constraints on the parameters of the martingale.
The multiplier is usually chosen at a maximal value of 2; those simple bets having a probability of winning close to ½ are preferred, such as red/black, even/odd, or low/high (this condition makes the martingale suitable for other games, such as blackjack or baccarat). As for the initial stake, it is, of course, up to each player but only relative to his or her bankroll and the player’s level of afforded risk.
Second, a solid bankroll might not be enough for playing the martingale effectively because most casinos have an upper limit for the stake of a bet; if that limit is reached within the succession of failures, your martingale cannot go through.
It then appears necessary for the player taking that risk to evaluate his or her bankroll against the possible failures, to check for the casino’s upper limit for a stake, to calculate or simulate the possible losses relative to the various initial stakes, and to choose the best option with respect to his or her strategy prior to playing the martingale.
The “Pessimistic” Math of the Martingale
Apart from the practical constraints above, mathematics itself still has something to say against the idea that the martingale is always a winning strategy. If algebra gave the impression that this is the case, for probability theory, the martingale is a bet like any other and submits to the same universal probabilistic laws.
Like any bet, a martingale has its own expected value. For the classic version with 2 as the multiplier, the expected value of the martingale is EV = S [ 1 - (2q) n ], where S is the initial stake, n the number of successive bets lost, and q the probability of winning the simple bet. Assuming q < ½ (the case in our color bet example), the EV is positive, which supports the algebraic result that you always make an overall profit with the first winning bet. So, if you have unlimited resources (and if the casino has no betting limit), you could, in principle, make money using such betting systems, but of course, none of these conditions are true in real life.
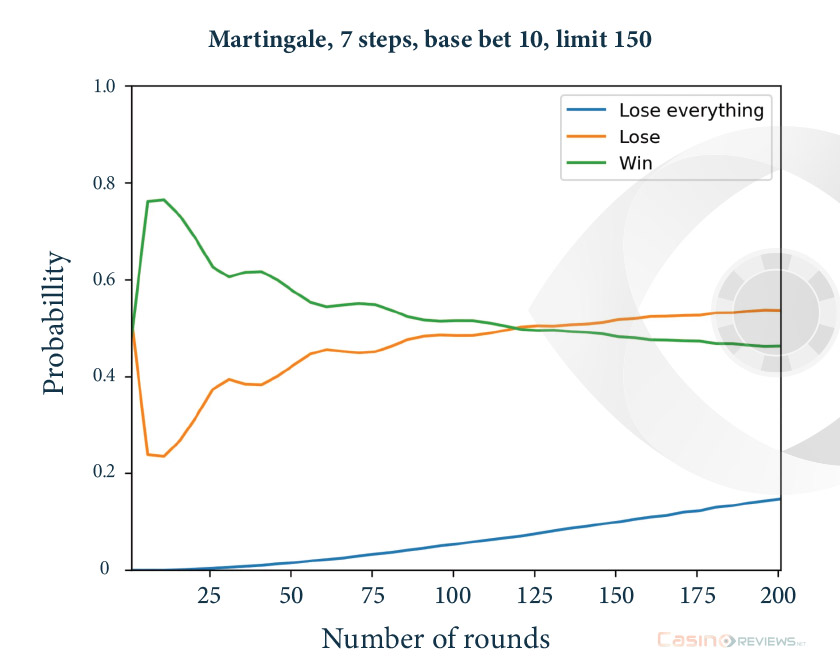
Moreover, there is a small theorem in game theory called the gambler’s ruin, according to which a persistent gambler who raises their bet to a fixed fraction of their bankroll after a win but does not reduce it after a loss will eventually and necessarily go broke, even if each bet has a positive expected value (which is the case with the martingale in our example).
Six Reds in a Row? Really?
In addition, all the algebraic calculations were supposed to reflect the profit over a finite (whatever long) series of plays. However, probability theory does not like and does not deal much with finiteness. All the statistical averages reflect a potential infinity of the experiments in which probability operates in a condition of randomness and not any arithmetical means. This principle does not support the belief that a long succession of failures is highly unlikely to happen now or in the near future, known as the gambler’s fallacy. The law of large numbers may make randomness look like an “ordered” disorder, but that order is only “visible” at infinity.
If we look at the probabilities, a succession of just four numbers of a certain color in roulette has a probability of 1/16, and one of six such numbers has a probability of 1/64—pretty low indeed. Still, such events or even less probable events occur all the time, and when they do, they may cause the cancellation of the player’s previous cumulated profits or even the player’s ruin, especially when s/he plays the martingale constantly. This is a reason for which the martingale is qualified as an “aggressive” betting system; it is aggressive in both directions—for the player’s bankroll and against the house.
When playing the martingale, you should not rely heavily on the low probability of repetition. In general, in gambling, probability alone is not the only thing that counts; one should also consider how probability is related to other statistical indicators, which involve profits and bankroll. In the martingale, the latter are essential.








Review this Blog
Leave a Comment
User Comments
comments for Gambling Math in Action – The Martingale Betting System in Roulette