The Mathematics behind Roulette

Despite the simplicity and transparency of the game, the mathematics of roulette involves elementary to advanced mathematical structures and models based on the set of placements allowed to be made on the table for the roulette bets. Knowing the mathematical facts of roulette betting – from probabilities and expectations of the simple bets to the profit function of the complex bets – can help players organize and improve their betting strategies while relying on objective information.
Introduction
Handling the coverage and composition of a complex bet and adjusting the stakes to reach certain balances between the probability of winning, expectation, and a satisfactory profit rate is one of the effective mathematical applications possible in roulette betting. Another application is identifying equivalent bets for a given bet, which allows players the possibility of choice with respect to strategic criteria, such as money management.
Not ignoring a game’s background mathematics is the adequate approach of a mathematically conceived game such as roulette.
With a history of over 220 years in the current form, roulette remained one of the most popular casino games. One of the features contributing to its popularity is the game’s transparency – all its elements are exposed to the players: the numbers on the table and the wheel and the ball landing; no hidden cards to guess in one’s hand (like blackjack or poker), no secret parametric configurations for its outcomes (like slots), and no strategy influencing the course of a game – we just place our bet and wait for the ball to land.
Easy Roulette Mathematics for Probability, Expectation, and House Edge
This transparency, along with roulette rules, allows for easy calculation of the odds involved. You don’t have to be a mathematician to know that the probability of the ball landing on a certain number is 1/37 or 1/38 (for the European and American roulette, respectively), and for a bet that includes many numbers, the probability increases as multiplied by the number of numbers you have placed your chips on, since those numbers are different and have the same likelihood of occurrence (or, in probabilistic terms, the elementary events of those numbers occurring are mutually exclusive and equally probable).
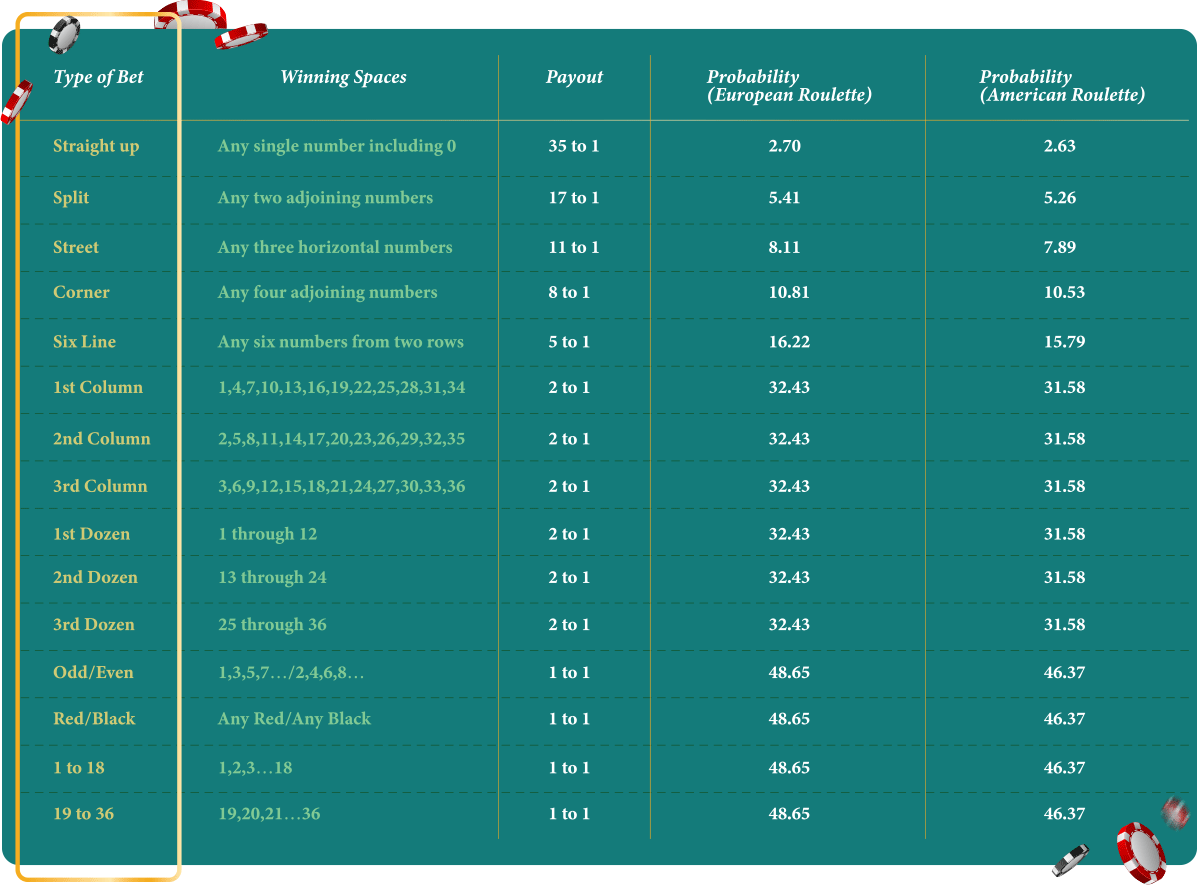
For instance, a street bet would win with a 3/37 or 3/38 probability (or 8.10% or 7.89% as a percentage, respectively) and a dozen bet with a 12/37 or 12/38 probability (32.43% or 31.57%, respectively).
Knowing the probability and the payout schedule, one may easily compute the mathematical expectation or expected value of any bet, that is, the average amount to win or lose over the long run for that bet. For example, a dozen bet with a $1 stake at European roulette has an expectation of 12/37 × $2 ˗ 25/37 × $1 = ˗2.7 cents. In general, the expected value (EV) of a bet is defined as follows:
(probability of winning) × (payoff if you win) + (probability of losing) × (loss if you lose).
This formula employs the probabilities of the events of winning and not winning the bet, the payout (2 to 1 in our example), and the amount of that bet (stake), and our result reads as follows: If one runs this bet an indefinite number of times, they are expected to lose on average 2.7 cents for every dollar bet.
In probability theory, that “average” means a limit (associated with the convergence of an infinite sequence) and not actually an arithmetic mean as it may seem in the above calculation. This meaning is given by probability (as a function), which is present in the formula of the mathematical expectation. In general, probability theory provides us with results obtained in ideal mathematical conditions, which assumes infinity as a feature of several mathematical notions.
Such conditions are not reproduced in the real world, where all our gambling experiences are finite. This is why we must not take literally the mathematically related concepts of “expectation” and “average”. They reflect a mathematical measure and not an accurate prediction. That is, one may actually lose less or more than the 2.7 cents for a dollar bet placed in 1,000 games or more. Only if it were possible for players to play that bet infinitely many times, the cumulated loss would be exactly at that rate.
Coming back to the calculated expectation, if we were to calculate it for any other type of basic bet (straight, split, street, color, etc.), we would find the same rate of 2.7 cents lost for a dollar bet (a negative expectation). This happens because the payout schedule of roulette is chosen for the expectation for all these basic bets to be equally at that rate.
Removing the currency, this rate of 2.7% is what we call the house edge of the European roulette (for the American roulette, the house edge is about 5.26%). House edge is defined as the opposite of the expected value and reflects the rate of the profit that the house makes over the long run from the players’ bets. Observe that for just one additional number (the double zero), the house edge gets almost doubled for the American roulette. A positive house edge refers to the house’s mathematical guarantee not to be ruined over the long run.
With a wheel with 37 or 38 numbers to choose from, this game apparently has easy mathematics behind it – numerical additions, subtractions, multiplications, and divisions for computing probabilities to win and expectations that anyone can do. What to do more with those numbers on the wheel? Suppose you add them together (from 1 to 36). In that case, you will get 666, the “number of the Beast”, but of course, this has nothing to do with roulette mathematics, but with a legend saying that François Blanc (one of the two brothers that added 0 to the roulette wheel in 1842) supposedly bargained with the devil to obtain the secrets of the roulette (Strzalko et al., 2009, p.5).
So, is roulette mathematics as simple as it may look? Given that roulette is not a combinatorial game (that is, a game whose final outcomes are combinations, like in card games or slots) and its sample space consists only of the numbers on the wheel as elementary events, and it is not a strategic game either, one may be inclined to answer yes. However, moving the view and focus from the wheel to the roulette betting table will reveal interesting things that may involve a bit more advanced mathematics.
Roulette Table: Placements, Bets, and Mathematical Structures
Another element contributing to roulette popularity as a game of chance is the freedom in placing bets. If we talk only about simple bets (we call simple a bet that is made through a unique placement of chips on the table), there are 154 possible placements allowing for such bets (all the known inside and outside placements – straight-up, split, street, corner, etc.).
However, let’s consider a bet made by multiple placements at once, with various stakes (call it a complex or combined bet). The possibilities for such combined bets in regard to placement are in a huge number, namely 2 raised to the power of 154, which is a 47-digit number!
Everyone may spread their chips everywhere on the table and with any coverage, but obviously, placing combined bets cannot be done chaotically in a game. For a trivial instance, no one will fill up an American roulette table by placing 38 straight-up bets (on all numbers) with the same stake (say $1), as they would lose no matter the outcome. Indeed, since one number wins and the other 37 lose, the “profit” for that bet would be 35$ ˗ 37 × 1$ = ˗2$. We call such a bet (resulting in a loss no matter the outcome) contradictory.
Or assume you want to place a straight-up bet on each number from 1 to 18 and a bet on High, with a higher stake. How many times should the stake on High be higher than the straight-up stake for the bet not to be contradictory? This turns into a simple algebraic equation and inequation to solve, giving the result: The multiplier should be any number but 18.
Is there a set of norms limiting the possibility of placing the bets in the players’ favor? How can we decide which bets are worth it and which aren’t? How would we choose our bets in a game from a huge number available? How can we optimize our bets and by what criteria? Roulette mathematics can answer all these questions.
A simple bet B can be viewed as a mathematical object in the form of a triple (A,pA, S), where A is the placement of the bet (like the set of numbers covered by that bet, called the coverage of the bet), pA is the payout rate associated with A (pA can only take the values 1, 2, 8, 11, 17, and 35 according to the rules of roulette), and S is the stake. Then, a complex bet can be represented as a family of simple bets (Ai, pAi, Si)i.
For every bet B (either simple or complex), a function can be defined on the numbers of the roulette with values in the real numbers, called the profit function of bet B. This function reflects the profit or loss of bet B, depending on the outcome of the spin and its expression holds the coverages (actually, the characteristic function of those sets), the payout rates, and stakes of the simple bets that bet B consists of. Based on the profit function, a relation of equivalence between bets can be defined, which significantly reduces the number of possibilities for the placements (Bărboianu, 2007, pp. 22-53).
From this profit function and its properties, whole mathematics applied to roulette develops and organizes the placements and bets into well-known mathematical structures – algebraic and topological structures. Using the mathematical properties of these structures, we can understand how to choose, adjust, or transform our bets so that they fit our strategy of playing roulette, in other words, to improve our bets.
In roulette, there is no optimal play (like in blackjack, for example), and any strategy is mostly subjective, reverting to choices. Mathematics can help players make these choices by giving them all the objective information associated with their personal betting system or behavior and offering alternatives for choices, along with their mathematical data. For example, the best choice between two or more equivalent complex bets is for that bet whose coverages (of the simple bets it consists of) are mutually exclusive (called disjointed bet), because of criteria related to money management over a series of plays and the enlargement of the coverage relative to the budget.
Why Rely on Mathematics When Playing Roulette
Whatever the simple or advanced mathematical structures that underlie roulette betting, one may still tend to ignore it, while looking at a roulette wheel and knowing that all those numbers arranged circularly have the same well-known likelihood of occurrence, as well as at the roulette table, where they are arranged symmetrically. But guess what: despite such equality and symmetry, roulette numbers do not have the same status.
This is just because on the table, we cannot cover any group of numbers with unique placements of the same type. For example, while 7 and 8 can be covered with a split bet, 7 and 12 cannot; the latter can be covered with a line bet, a First Dozen, or a Red bet, which have different payouts from a split bet. Therefore, because of the table configuration, not all numbers have the same status concerning possible placements.
The mathematics of roulette betting takes into account this fact, and this non-equivalence between roulette numbers can be mathematically speculated with regard to strategy.
The basic contribution of mathematics to the game of roulette (as with any other game of chance) is the mathematical information associated with every bet, namely measurements in the form of odds/probabilities and expectations in the form of averages and effective values of profit (or loss), depending on the outcomes and the various betting strategies or systems. It almost sounds like an ethical requirement for someone to expose such information in any game of chance.
Surprisingly, roulette offers the highest probability of winning among all games of chance; we can find bets with over 90% winning probability. Indeed, such probability increases with the coverage of a bet. For instance, a complex bet consisting of 17 straight-up bets on black numbers with a stake of $1 each and a bet on Red with a stake of $18 has a 92.09% probability of winning. But don’t be too excited about this: winning on either number or color will make you a profit of only $1.
While you can still be satisfied with this and run this bet repeatedly, a possible failure would cost you $35, which would cancel 35 of your assumed previous profits. The expected value of that bet is – $1.84, expected to lose on average for the $35 bet, despite the huge probability of winning. This is actually at the rate of the house edge of American roulette, but even in the case of profit, the profit rate (relative to stake as an investment) is only about 2.85%. It’s all in the profit function of that bet.
Probabilities of winning are always counterbalanced by expected values, which depend on the payout rates of the game, and it is natural to be this way for the house edge to be maintained. In general, the mutual balances between probability, expected value, and stake are the objective criteria based on which we can derive the optimal play of a game (if possible) and build our strategies. Mathematics helps us organize such information and make it applicable and effective. It is in the nature of mathematics to organize our thoughts in the most rigorous way possible. Good organizing always leads to gain in time and resources, no matter the domain of activity.
This is also the case for roulette. Besides organization, mathematics also has other roles, such as confirmation and optimization; in roulette, these roles guarantee players that whatever would be the ultimate result of their short- or long-term play (winning or losing), the information that they needed for their play are accurate, available, and perhaps have followed the right models since mathematical truths cannot be questioned.
Conclusion
Roulette was invented by mathematician Blaise Pascal, the early father of probability theory, and was further developed with the support of the examples and applications from games of chance, including roulette. Also, the famous progressive betting systems based on algebraic models (Martingale, D’Alembert, etc.) were first discovered and tested at roulette before being applied to other games. As such, roulette will never be mathematics-free.
We must neither fear nor avoid the mathematics behind roulette. In fact, one may not need to grasp it in depth but just have the mathematical results in an applicable, user-ready form. This won’t guarantee any wins, but it will ensure the right approach to a mathematically conceived game.
References:
Strzalko, J., Grabski, J., Perlikowski, P., Stefanski, A., & Kapitaniak, T. (2009). Dynamics of Gambling: Origins of Randomness in Mechanical Systems (Vol. 792). New York: Springer Science & Business Media.
Bărboianu, C. (2007). Roulette Odds and Profits – The Mathematics of Complex Bets. Craiova: Infarom.








Review this Blog
Leave a Comment
User Comments
comments for The Mathematics behind Roulette