Mathematical Fairness of Slots – How to Calculate If a Game Is Fair

We got used to taking the statistical indicators RTP and volatility as criteria for choosing a slot game, but this was because they were the only indicators available (and yet not for all the games). The PAR (probability accounting reports) sheets, which provide the entire parametric configuration of a game, are kept secret by the slot producers, and this information, for some games, was obtained only through legal intervention or when the information was made public.
In this article, we will talk about a more precise indicator called mathematical fairness, which can be computed only if we know the probabilities of the winning combinations.
Payout Schedule, Probability, and Mathematical Fairness
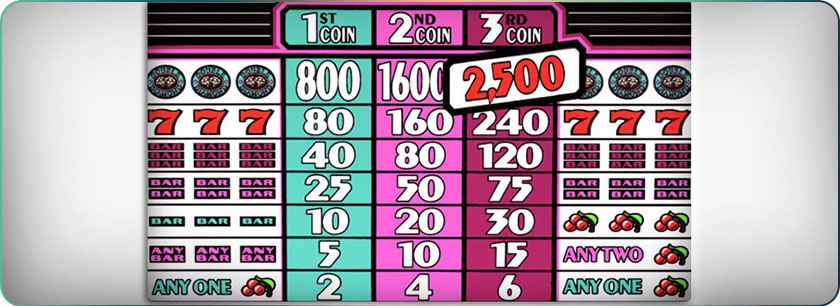
As an example, let’s say a slot game has in its payout schedule three prizes with the following associated parameters:
For such a game, we know its parametric configuration, but the above parameters indicate a kind of skinning of money, at least for Prizes 1 and 3. For Prize 1, the game pays only 1,000 times the credit for a 1-to-6,000 probability (in frequential terms, 1 in 6,000 spins on average, which is 6 times as high as the number of non-winning spins paid back with that prize).
For Prize 2, the game pays only 500 times the credit for a 1-to-800 probability (in frequential terms, 1 in 800 spins on average, which is 1.8 times as high as the number of non-winning spins paid back with that prize). For Prize 3, the game pays only 10 times the credit for a 1-to-50 probability (in frequential terms, 1 in 50 spins on average, which is 5 times as high as the number of non-winning spins paid back with that prize).
In brief, the game offers, for some prizes, a very low payout rate with respect to the likelihood of winning and implicitly with the average loss. In terms of expectation, for Prize 1, we expect to lose on average about 83% of the credit bet; for Prize 2, about 37%; and for Prize 3, about 78%. Such figures make us ask ourselves how fair that game would be in comparison to other games. In other words, what would be the mathematical fairness, and how should it be computed?
Mathematically Fair and Mathematical Fairness
A mathematical relation between probability and payout rate accounts for an adequate concept of fairness of a bet as a statistical indicator. Let us first define what it would mean for a bet to be absolutely fair.
A bet is called mathematically fair if its expectation is 0 (like a bet on heads or tails at a coin toss with a payout rate ×1: EV = (1/2) × c − (1/2) × c = 0, where c is the stake and 1/2 the probability of either heads or tails).
In general, if p is the probability of winning and r is the payout rate of a bet, the bet is mathematically fair if and only if r = (1 − p )/p (in this case, r is the fair payout rate). This is a necessary and sufficient condition for the EV to be null. In our slots example, the bet for Prize 1 would be fair if its payout rate was ×5,999, about 6 times as high as the actual rate.
However, classical games of chance played in casinos do not consist of any mathematically fair bet since that would not guarantee the house edge as a profit for the house (this is why I called the attribute absolutely fair). We can accept that in gambling, as in any business, the company has to sell products or services at a higher price than the purchase price to make a profit, and this also applies to bets.
However, the surplus value added to the price is subject to certain limits that are settled by the market itself and sometimes by official regulations. In slots, neither that surplus nor the buying price is transparent once we have no access to the parametric configuration of the game. Also, even if that configuration were made public, the producer would not display the winning probabilities on the game’s interface; we would have to compute them ourselves.
The fairness 𝑓 of a bet is given by the ratio between the actual payout rate r of that bet and the fair rate: 𝑓 = rp/(1 − p). The higher the value of this fraction (the closer to 1), the fairer the bet. In our example with Prize 1, fairness is calculated as follows: 𝑓 = 1,000 × (1/6,000)/(5,999/6,000) = 0.166 or 16.6%. As such, the mathematical fairness of a bet represents in fraction or percentage a measure relative to the absolutely fair bet with zero expectation. We can also define the fairness of the game as the product of all the fairnesses relative to each bet. Of course, the fairness of a game decreases with any unfair bet in its payout schedule.
Computed Fairness in a Real Example
Let us see now what the fairness of a bet in a real slot game is, for which the PAR sheet is available. I took as an example the IGT game Lucky Larry’s Lobstermania, a five-reel game with 47 × 46 × 48 × 50 × 50 stops on the reels and the symbol weighting given in its PAR sheet. The PAR sheet was obtained through the Freedom of Information and Protection of Privacy Act in Canada (Harrigan & Dixon, 2009). Let’s take three specific prizes from the payout schedule of the first version of the game:

The probabilities in the last column were computed by dividing the number of combinations of stops giving the winning combination to the total of the 47 × 46 × 48 × 50 × 50 = 259,440,000 possible stops combinations. According to the general formula in the previous section, the following apply:
- For Prize 1, the mathematical fairness is 𝑓 = 1,000 × 0.00001930/(1 − 0.00001930) = 0.0193 or 1.93%.
- For Prize 2, the mathematical fairness is 𝑓 = 500 × 0.00005044/(1 − 0.00005044) = 0.0252 or 2.52%.
- For Prize 3, the mathematical fairness is 𝑓 = 30 × 0.00060179/(1 − 0.00060179) = 0.0180 or 1.80%.
As a reference example for comparison, take a color bet in European roulette. Its probability of winning is 48.64%, and its payout rate is ×1, and hence, its fairness is 94.70%. For a column bet, the payout rate is ×2, and the probability of winning is 32.43%, so its fairness is 43.82%. For a straight bet, the payout rate is ×36, and the probability of winning is 2.7%, so the fairness of this bet is 94.57%! Roulette is a very reasonably fair game compared with slots.
Fairness as Another Criterion of Choosing a Game
In the situation (rare, indeed) in which we know the parametric configuration of the slot game we intend to play, we can compute the probabilities associated with all the winning combinations generating prizes (or take them from specialized tables of probabilities). It is the most important information of the game, which can be translated into frequential terms.
For instance, a probability of 0.01 (1%) for a certain winning combination on a payline means that you have to play on average 100 games to hit it once. This information, paired with the payout for that hit, is the most objective measure for assessing whether that bet is worth placing, including the time and money spent in the game.
All those probabilities of the winning combinations yield the RTP, but knowing their values individually is much more valuable than the RTP alone. You may choose among certain games based on one or more such probabilities even though the chosen game does not have the highest RTP. As for volatility, knowing the parametric configuration allows the computation of the variance over a definite interval, so you no longer have to guess at it.
There is no absolute boundary between “normally” unfair and highly unfair, and any delimitation is subjective; however, comparisons among slots may generate objective criteria for choosing. Between two bets with approximately equal probabilities of winning, it is advantageous to choose the fairer; between two games with not-too-different probabilities of winning, respectively, it is advantageous to choose the fairer.
Applied to slots, this criterion works independently of the RTP choice. Although low payouts with respect to probability are reflected in a low RTP, a player may have as a target a specific prize of the game and not the entire schedule—say, Prize 3 in our examples, especially if the player intends to play for a limited time. If that bet is highly unfair and the rest of the prizes are not, compensating the decrease in RTP, the player may choose another game where a similar bet is fairer, regardless of the RTP.
Of course, all the strategic choices discussed are applicable only if the parametric configuration of a game is known.
References:
Bărboianu, C. (2022). Understanding Your Game: A Mathematician’s Advice for Rational and Safe Gambling. Târgu Jiu: PhilScience Press.
Harrigan, K. A., & Dixon, M. (2009). PAR sheets, probabilities, and slot machine play: Implications for problem and non-problem gambling. Journal of Gambling Issues, Vol. 23, 81–110.








Review this Blog
Leave a Comment
User Comments
comments for Mathematical Fairness of Slots – How to Calculate If a Game Is Fair