The Coverage of a Roulette Bet – The Math of Spreading Chips on the Table

A couple of elements that make roulette such an attractive game of chance are the freedom that the players have in placing their bets and the wide range of possibilities for their bets to cover whatever numbers or groups of numbers on the roulette table. Thus, the question arises as to whether we should spread our chips arbitrarily or chaotically on the table (since we are allowed to do that) or somehow organize this combined betting in our favor. An immediate reason in favor of the latter alternative is technical.
Each roulette game has its own chip division in smaller amounts as well as a minimal and maximal stake required for some bets (for instance, an outside bet is likely to have a minimal stake required and a straight bet a maximal one). Therefore, a multiple placement of bets is constrained by such division and the house rules relative to the money management of the player. The smaller the division of chips, the more numbers we can cover with our multiple or combined bet relative to our wagering fund.
However, this is not the only reason for a convenient organization of our betting. Other reasons are provided by the mathematics of roulette, which provides the criteria of such organization as well.
Placements, Sets of Numbers, and Coverage of a Roulette Bet
We call a placement any choice to place a simple bet (straight up, split, street, etc.) on the roulette table for one spin in regard to numbers by putting the chip or chips in one place, according to the game rules. For simple bets, we have 154 possible placements (one bet–one placement). However, if we count all placements for all possible bets, including the multiple placements of the combined bets, we get a huge number, namely, 2154. This is actually the number of possible choices for a bet regardless of the stake.
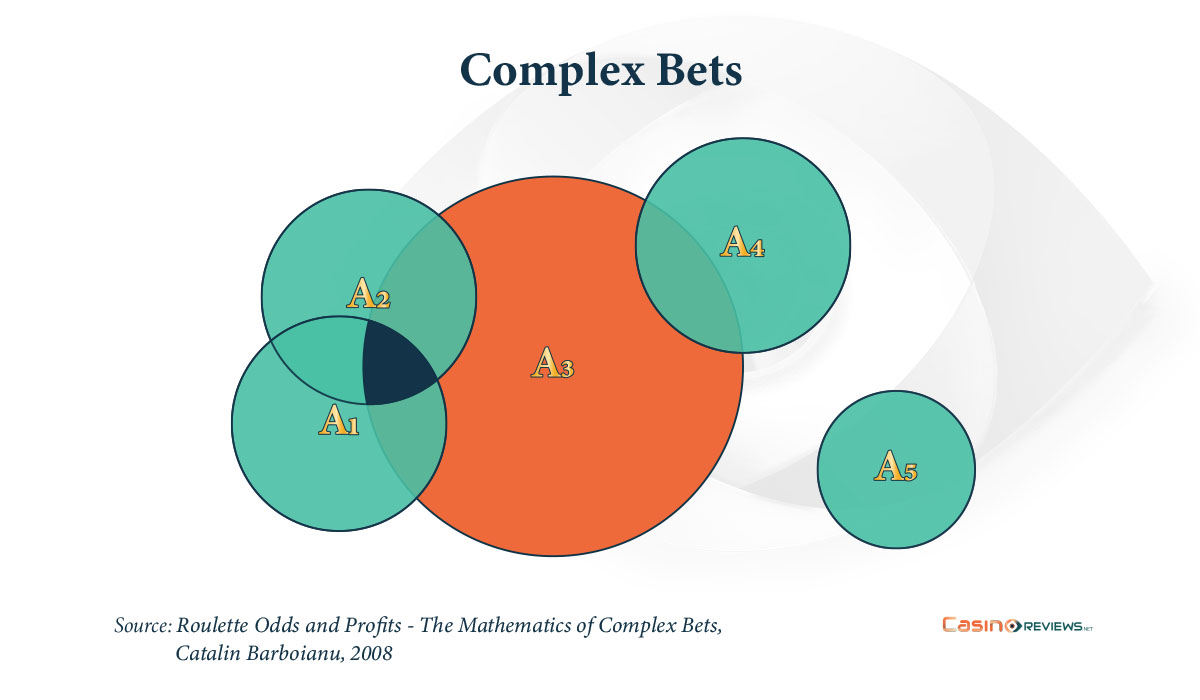
If we identify a placement with the set of numbers in that placement, roulette becomes a good provider of exercises for students who learn about sets in their math class. This is because placements can be exclusive or intersect one another and can be joined as unions or partitioned. The set of numbers that a bet is placed on is called the coverage of that bet. For instance, the coverage of a split bet on 18 and 21 (spl (18, 21)) is the set {18, 21}, which has two elements; the coverage of a bet on red is the set of all red numbers, counting 18 elements.
As for a combined bet, its coverage is defined as the union of all the placements of the simple bets it consists of. For example, the coverage of the combined bet B consisting of a bet on the first column and the street bet on (4, 5, 6) (denote it by B = (1stC, str (4, 5, 6))) is the set {1, 4, 5, 67, 10, 13, 16, 19, 22, 25, 28, 31, 34}, which has 14 elements, of which one (4) belongs to both constituent bets. The number of elements of a coverage A is called the length of A and is the cardinal of set A (the number of elements in A), denoted by |A|.
It is clear now that the length of the coverage of a bet accounts for the probability of winning that bet, which is the ratio between |A| and 37 or 38, depending on the type of roulette you are playing, either American or European roulette. In our previous example, the probability of winning bet B in European roulette is 14/37 = 37.83%.
Mathematical Constraints for Arbitrary Coverage
With the abovementioned formula for probability, one can easily derive that the larger the coverage of a bet, the higher the probability of winning the bet. Therefore, is filling up the roulette table with all kinds of bets just to cover as many numbers as possible (or as our wagering fund supports) a valid strategy? Not at all. Probability is not the only criterion for choosing one bet or another, and coverage is not the only parameter of a bet. If they were, roulette would be the paradise of gambling since it offers the possibility of bets with over a 90% probability of winning.
First of all, arbitrary placements just aiming at a large coverage may result in no profit whatever the outcome of the game. They are what we call contradictory bets. No one is supposed to place such bets; for instance, betting together $1 on each of the black numbers, 17$ on red, and $1 on zero will always result in either a loss (−$2) or zero profit, whatever number the ball will land on. The possible profit (or loss) of a bet is given by the profit function of that bet, and a first constraint for combined bets with large coverage is that their profit function should be positive for at least one outcome in that coverage.
However, some non-contradictory bets should be avoided or improved. These are bets whose coverages overlap. For example, take the bet (2ndC, cor (8, 9, 11, 12)) on the second column and on the corner with 8, 9, 10, and 11. The placements of those two simple bets overlap on numbers 8 and 11. Regardless of the stakes, the first observation is that having those two numbers in both coverages decreases the probability of winning for that combined bet in the sense that if one chooses another corner bet exclusive of the second column or another column bet exclusive of the initial corner bet, the probability of winning would increase with 2/37 or 2/38, while the investment remains the same.
The ideal outcome for this bet—in which 8 or 11 are hit, thus making the highest profit—does not justify the initial choice either; first, the probability of that happening is low, and second, if there is such a big confidence in any of those two numbers coming up, the player may place a bet separately on them, as a split or double straight-up bet, while excluding them from one placement (choosing another corner bet instead). In terms of investment, it is reasonable to save from the stake invested for a double covering of 8 and 11 and place another bet instead with that saved money.
From the book Roulette Odds and Profits — The Mathematics of Complex Bets.
Hence, as a general criterion of organization of combined betting in regard to placements, the coverages of the bets should be partitioned (that is, to have mutually exclusive placements that are joined together as the total coverage) as there is no mathematical or practical reason to overlap the placements.
Coverage and Bets with the Same Parameters
Take the following two bets: a split bet and a bet consisting of two straight-up bets on the same numbers as in the split bet—for instance, spl (4, 5) and (strg (4), strg (5)). The two bets have the same coverage {4, 5} and therefore the same probability of winning. Let’s see the expectation for each bet, say, in American roulette.
For the split bet, assuming a stake S, if 4 or 5 are hit, the profit is 17S and otherwise (as a loss) is −S; for the double straight-up bet, if one assumes stake S on each straight-up bet, the possible profit would be 34S or −2S (the loss). The expected values of the two bets are −S/19 and −2S/19, respectively. In all these calculations, the payout of each simple bet as well as the probabilities of winning and losing were involved.
Now observe that if we halve the stake of the split bet (S) and bet it on each straight-up bet (S/2) of the combined bet, we have the same possible profit, the same possible loss, the same investment, and the same expected value on the same sets of numbers as outcomes. These are what we call equivalent bets.
Of course, that split bet is equivalent to any other split bet with a different placement and with the same stake. This example is trivial, but there are equivalent bets of any complexity among those 2154 possible placements. Obviously, two equivalent bets have the same length of their coverages. The converse is not true as equivalence is defined through the profit function and, as such, also depends on stakes.
As a mathematical entity, a roulette bet is identified by its placements and the (partial) stakes associated with these placements (the payouts are implicit as each placement of a simple bet has a certain payout). Once we know that there are equivalent bets with the same total stake but different placements or with the same coverage but with different partial stakes, that total number of possible placements no longer seems so huge.
When choosing our bet, apart from confirming that it is not contradictory or does not have overlapping placements, we can also choose among several bets that are equivalent to it. The reasons for such a choice are related to everyone’s strategy of betting and can be either subjective or objective.
For instance, a subjective reason is related to the fact that numbers do not have the same status on the roulette table as they have on the wheel. Numbers 17 and 20 can be covered by a split bet, while 17 and 23 cannot; the only simple bet that can cover numbers 1 and 35 is the odd bet; instead, numbers 1 and 2 can be covered by many inside bets, while numbers 1 and 26 cannot be covered with one placement. Such examples argue for the necessity of choosing among bets, and this means organization.
If a player wants to cover his or her favorite numbers for some subjective reasons with bets of certain types and under a certain strategy, s/he is supposed to choose among types of bets and equivalent bets. There are also practical reasons for such choices. For instance, a player has limited time to place the chips before the next spin, so manipulating many chips of different values for a bet that assumes placing chips physically on many numbers or placements might result in not having all the chips placed until the next spin. In that case, it is recommended for that bet to be replaced with one equivalent to it, requiring fewer placements.
Conclusion
The important thing to note is that in roulette, betting coverage is important, but it is not the only factor that accounts for an objective analysis of the bets in relation to the player’s personal strategy. In fact, in roulette, the only strategy is that of choosing (placing bets is a choice) and adjusting the stakes of those bets to fit personal money management and objectives. The mathematics of roulette not only helps in organizing your bets such that your choice would be objective but also is the only provider of such objectivity.








Review this Blog
Leave a Comment
User Comments
comments for The Coverage of a Roulette Bet – The Math of Spreading Chips on the Table